23. 循环神经网络总结
我们来总结一下目前为止了解的知识:
22 循环神经网络总结 V7 最后一节
你已了解到,循环神经网络中,使用激活函数时,当前状态取决于的输入和之前的状态。
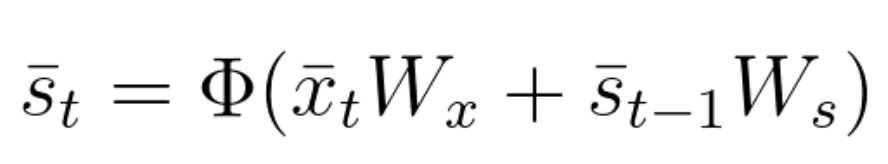
方程式 56
当前输出是当前状态要素及其对应权重矩阵的简单线性组合。
\bar{y}_t=\bar{s}_t W_y (不使用激活函数)
或
\bar{y}_t=\sigma(\bar{s}_t W_y) (使用激活函数)
方程式 57
我们可以使用折叠模型或展开模型来表示循环神经网络:
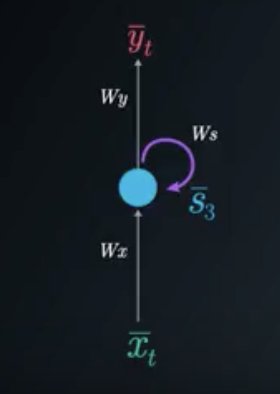
循环神经网络折叠模型
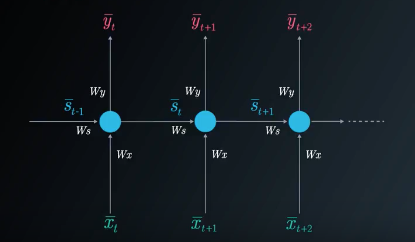
循环神经网络展开模型
在单个隐藏(状态)层的例子中,我们会考虑三个权重矩阵。这里我们使用下面的符号:
W_x:表示连接状态层和输出的权重矩阵。
W_y:表示连接状态和输出的权重矩阵。
W_s:表示连接之前时间步长状态和下一个时间步长状态的权重矩阵。
调整权重矩阵所需的梯度计算如下:
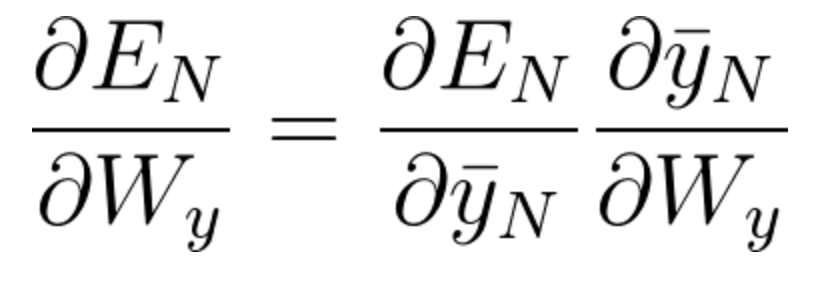
方程式 58
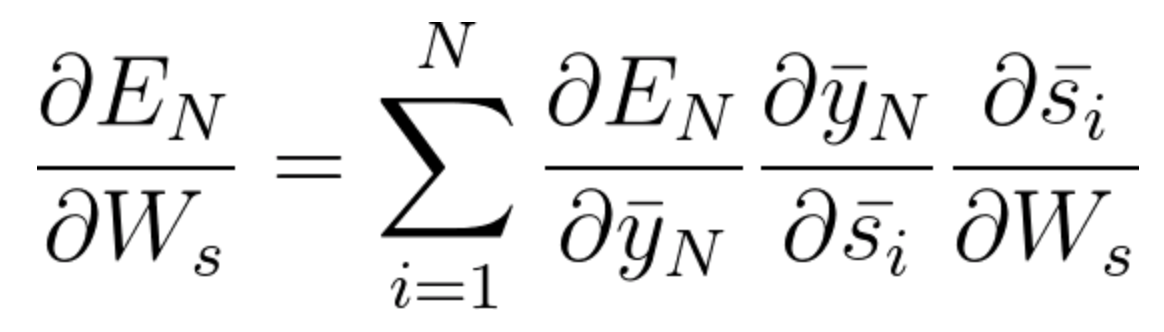
方程式 59
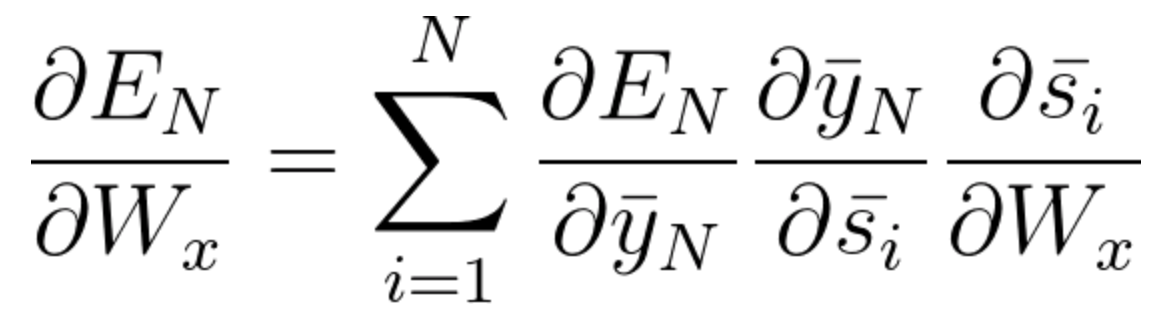
方程式 60
在方程式 59 和 60 ,我们使用了基于时间的反向传播算法,其中我们累加了之前时间步长中的所有贡献。
使用基于时间的反向传播算法训练循环神经网络时,我们可以选择小批量进行训练,这里我们定期更新批次权重(而不是每次输入样本)。我们计算每一步的梯度,但不要立即更新权重。另外,我们对权重每次更新固定的步长数量。这样有利于降低训练过程的复杂性,并消除权重更新中的噪音。
以下是使用梯度下降的小批量训练的方程式:
(其中\delta_{ij}表示每隔一次输入样本计算的梯度,M表示我们该过程中累加的梯度数)。
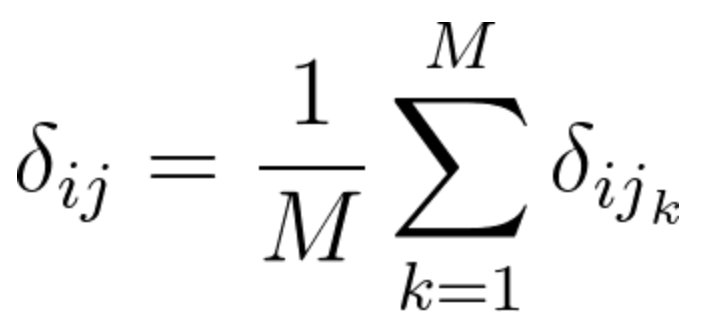
方程式61
如果反向传播超过10个时间步长,梯度会变得非常小。这种现象称为梯度消失问题,其中信息的贡献随着时间的推移呈几何衰减。因此,网络会忽视多个时间步长的时间依赖。长短期记忆网络单元专门解决该问题。
在循环神经网络中,我们可能也有相反的问题,称为梯度膨胀问题,其中梯度数值失去控制一样增长。梯度裁剪是解决梯度膨胀问题的简便方法。
更多梯度裁剪的信息可参考此处。
你可以关注简要描述梯度裁剪思想的算法1。